Devilliers/Grechkina thumped P. Smith/Jansen last Tuesday night at The Orchard.
I tracked success of third shots.
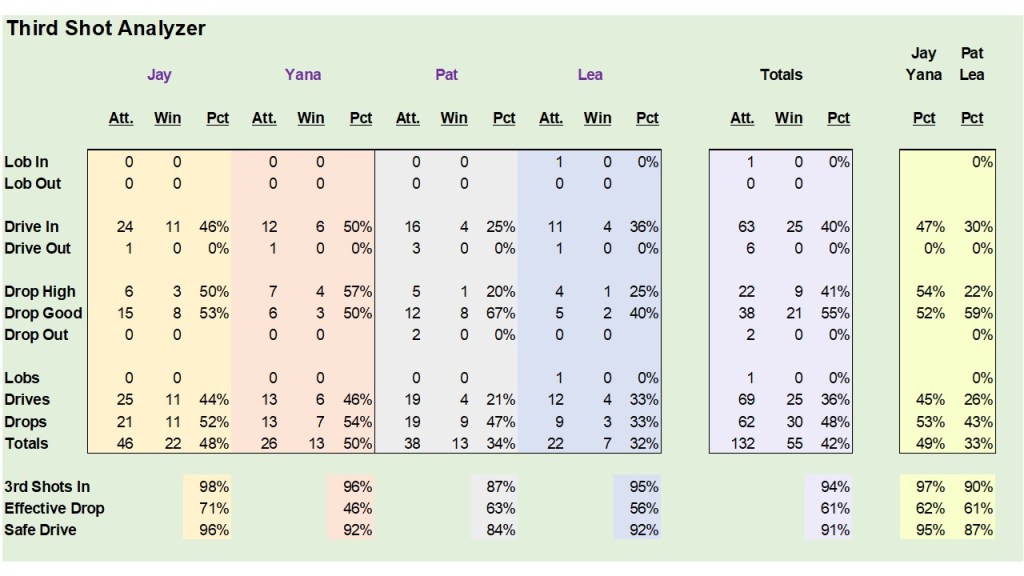
There’s a lot of stuff going on there.
If you look at Patrick’s stats, you can see reasons why they lost. When he hit a drive, he and Lea only won 21% of their points … Lea won 33% on her drives. Meanwhile when Jay hit drives, his team won 44% of points, when Yana hit drives, her team won 46% of points. Presumably Jay was able to clean up a lot of trouble following drives.
Pat Smith hit five thirds out … three drives and two drop shots, meaning just 87% of his thirds got over the net and were consequently hit by the opposition.
Effective Drops (taken off the bounce or with paddle below wrist) were interesting … Yana only hit 46% effective drops, but her/Jay scored on 57% of non-effective drops. Digging balls out of the transition zone is an important skill to master.
Across all four players, 41% of non-effective third shot drops resulted in a point.
Across all four players, 55% of effective third shot drops resulted in a point.
Intuitively, one would think that, yeah, getting your third shot drops down is a good thing, and it is a good thing. However, there were 22 third shot drops that were not effective … the math shows that 22 * (0.41 – 0.55) = 3 points … just three points … were lost by all four players across both games because third shot drops weren’t effective.
This is where life gets interesting …. if a player were to hit a lot of third shot drops into the net, the player would theoretically be more incented to hit thirds high, as the math would yield a better outcome.
Think of it this way. Say you play two games, winning each game 11-8. Say that a high third gives you a 40% chance of winning a point, an effective third gives you a 55% chance of winning a point. Say that 60% of the drops that get over the net are “effective”. Your team hits 50 third shot drops in the match. We can see how many “expected points” are generated based on how many third shot drops do not get over the net.
Let’s assume 60% of drops are effective, but 10% of drops hit the net. Expected Points = 50*0.10*0.00 + 50*0.90*(0.60*0.55) + 50*0.90*(0.40*0.40) = 22.05 expected points.
Let’s assume that 60% of drops are effective, but 20% of drops hit the net. Expected Points = 50*0.20*0.00 + 50*0.80*(0.60*0.55) + 50*0.80*(0.40*0.40) = 19.60 expected points.
Now, let’s pretend that 35% of your drops are effective, but none of the drops hit the net … they all get over, but most of them are high. Expected Points = 50*0.00*0.00 + 50*1.00*(0.35*0.55) + 50*1.00*(0.65*0.40) = 22.63 expected points.
In other words, you are better off with a lousy third shot drop that gets over but does not hit the net.
Think about that one the next time somebody tells you that your thirds shots aren’t good enough.